| Author | Message | ||
| 82daion
New Username: 82daion Post Number: 1 Registered: 5-2005 |
Does anyone know the cutoff frequency for the filters in Alembic electronics? Just curious. | ||
| mica
Moderator Username: mica Post Number: 2546 Registered: 6-2000 |
The range is from 350Hz-6KHz. | ||
| 82daion
New Username: 82daion Post Number: 2 Registered: 5-2005 |
Thanks. Do the filters cut off at 3db/octave? | ||
| mica
Moderator Username: mica Post Number: 2553 Registered: 6-2000 |
The slope is 12dB/octave. | ||
| goatfoot
Member Username: goatfoot Post Number: 70 Registered: 12-2003 |
I'm no audio expert but that means that everything above 6 KHz is effectively filtered out when the filter is fully off. Correct? So does that mean that there are some upper harmonics that are always cut off on a bass with a filter/q elec package? I'm asking because I'm seriously considering adding a filter/q to my custom bass with Orion elecs (v/p/b/t). I like the way the bass sounds set "flat" but I would like the additional flexibility that the filter/q would add. So would adding the filter/q change the way the bass sounds "flat" if I set the filter and q fully off? Thanks, Kevin | ||
| adriaan
Senior Member Username: adriaan Post Number: 571 Registered: 6-2002 |
Kevin, You set the filter's cut-off frequency by turning the filter knob. Everything above that frequency is gradually dampened. Filter fully open sets the cut-off frequency at 6 KHz - so we're not talking about root notes. Filter fully closed is at 350 Hz - we're already way up on the fingerboard of a bass. The closest to "neutral" that you can get is with the filter fully open and with the Q switch in neutral. A low-pass filter always produces a slight "bump" in the spectrum at the cut-off frequency, so even if the filter is fully open then it is not completely neutral. When you engage the Q switch, then the bump is even more pronounced - produces a bit of "twang". Ask someone to turn the filter knob (with the Q engaged) while you're playing, and you'll notice a wah effect. (This is palembic's infamous third arm.) | ||
| bob
Senior Member Username: bob Post Number: 464 Registered: 11-2002 |
Kevin, Most of us contend that there are no useful harmonics for a bass (with at least up to a high C string) above 6 Khz, so you should not be concerned about losing anything. Keep in mind that many Alembics always have the filters in circuit, and have for a very long time now. -Bob | ||
| 82daion
New Username: 82daion Post Number: 3 Registered: 5-2005 |
Thanks for all the info, everyone. It's nice to join such a knowledgeable board. | ||
| davehouck
Moderator Username: davehouck Post Number: 1950 Registered: 5-2002 |
Kevin; in addition to what Adriaan and Bob said, the cutoff at 6KHz is not square but rolls off at 12dB per octave if I recall correctly. edit: Whoops, Mica already said that! (Message edited by davehouck on June 23, 2005) | ||
| sfnic
Member Username: sfnic Post Number: 80 Registered: 3-2005 |
And yes, for the purests who insist that there is harmonic information above 6k in a bass, there certainly is. And it certainly colors the instrument's tone. However. Time for a giant pile of arithmetic and assorted acoustic physics. (Exceptionally long post warning) Let's look at a basic 4-string, 24-fret bass. The highest fundamental frequency it'll produce is about 390Hz (G-string, 24th fret). 6KHz is another four octaves above that. From a raw mechanical perspective (-6/octave), that's an overtone that's about -24db from the highest regular fundamental before the filter ever kicks in. So, again leaving out the filter, the next octave point (12KHz) is about -30db, and the last octave point (24KHz) is about -36db. So, even though there is string energy present above 6k, it's generally more than 24db down from the highest fundamental a 4-string can produce, leaving aside the pickup response. We don't really need to worry about this rolloff, though, as it represents "what the string is doing." Which is, after all, what we're trying to accurately reproduce. It merely addresses the question of "what's present above 6KHz" before adding in any additional losses the instrument system may impose. (Also, "what's above 6KHz" includes some incredibly nasty crap such as thermal noise and RF interference. If we're going to play in that space, we'll need to be able to separate signal from shit. More on that later.) Now, let's factor in the pickups. There are three factors involved in determining a pickup's frequency response. First, its electrical characteristics as coupled to the amplifier chain. Coil inductance, capacitance, impedence, loading, etc. Let's ignore that for the moment, since that varies from pup to pup. Second, the pickup's magnetic aperature. Again, this varies from pup to pup, so we'll leave that alone for a sec as well. Finally: pickup placement, relative to the vibrating string. This may actually have the greatest impact on an instrument's tone, beyond its mechanical construction. A pickup is only looking at a small section of the string, and so only a particular subset of the overtone sequence being generated by the instrument. That subset represents a collection of energy resources that differ in frequency, amplitude and phase. It's the phase/amplitude relationship that's of concern here. Basically, the pickup's aperature and placement act as elements of a mechanical filter that rejects any part of the string's harmonic structure that it can't see. So the phase and amplitude of the individual harmonics create sum-and-difference resonances that ultimately result in a comb-filter. Looking at our G24 note at 392 Hz, with a pair of pickups each with a 1 inch aperature, sitting 3.75" and 7.5" from the bridge, respectively. Both pickups are at full volume. The resulting response curve shows a +6db peak at about 1.1KHz, followed by a fairly sharp notch (-60db) an octave higher at about 2.2KHz. So, just in the pickup aperature and location, there's already a 60db/octave rolloff about 2/5 octaves above the fundamental! Of course, as a notch, there's energy above that node point as well. The next peak occurs at about 3.3KHz, which sits about -9db from the fundamental. There's another -60db notch at about 3.85KHz, followed by another -9db peak at about 4.4KHz. Finally, there's another peak at just about 6KHz that's of equal amplitude to the fundamental. The general effect is to create a response hole between 2.2KHz and 4.4KHz, where there's very little support for whatever string information is actually there, and which creates an upper hinge point of about 6.6KHz, after which the peaks within the comb filter roll off at about 6db. So, _mechanically_, this instrument shows a 6db/octave rolloff low-pass response with a 6.6KHz pole, when reproducing a 392Hz fundamental. Again, this is _before_ adding in the pickup's electrical characteristics; this is purely the pup's location and aperature. Let's look at the other end of the spectrum: an open E string at 41Hz. Same pickup setup as above. The resonant peak hits at about 125Hz; first comb notch hits at about 250Hz; etc. The mechanical filter here has its low-pass hinge at about 2KHz, again with a 6db/octave rolloff. So, mechanically, the instrument displays a self-variable low-pass response, with the filter "opening" as the fundamental note increases in pitch. NOW, add in the pickup's electrical response. A pickup will generally have a resonant frequency, above which it naturally rolls off. A classic passive Fender pickup will have a resonance (when installed and loaded with volume and tone pots and used with a cable) of about 2.5KHz (give or take .5KHz), above which it'll roll off at about 6db/octave. A low-impedence active pickup, such as Alembic builds, will have a resonant peak somewhere between 4KHz and about 7.5KHz, depending on how low-Z is really is, and how much gain the designers are making up in the preamps. (Again, we're leaving out any preamp filtering, so far, and are merely looking at the total harmonic energy available in the system.) Putting all the above stuff together: The string rolls off at 6db/octave from the fundamental. The instrument rolls off at 6db/octave from the pickup's position/aperature low-pass hinge point. The pickup rolls off at 6db/octave from its resonant peak. So, let's take a bass, playing an open G string (roughly 100Hz). Low-Z pups with aperature and location specs as described above, and a 5KHz resonant peak. What do we have? The string rolls off at 6db/octave above 100Hz. The instrument rolls off at 6db/octave above 3KHz. The pickup rolls off at 6db/octave above 5KHz. That gives us an aggregate signal of (-36 plus -6 plus -3) equals -45db down at 6KHz. Go up another octave and you're down -63db at 12KHz. That's a real long way down, for the "next to last" octave, let alone trying to squeeze 20KHz out of the system. That's all there is. To get anything else out of the system, (i.e., to get back to the raw string's response) you'd need to provide boost to offset the instrument's mechanical rolloff and the pickup's electrical rolloff, or about 9db at 6KHz (remember that number, btw.) and about 21db at 12KHz. That'd take roughly a four-pole 15KHz high-pass filter. Take half a second and think about what else would be getting amplified by 21db or more, and then remember how much effort RonW has put into keeping noise and radio frequency interference OUT of Alembic's instruments... So, let's add in Alembic's active filters. Rather than trying to boost the last two octaves, where there's very little information to begin with, and which will give us at least +21db of noise gain, let's see what we can do to at least try to recover some of that string response that's being eaten by the electro-mechanical structure of the bass itself. Remember that 9db number I mentioned above? It's not a coincidence that Q-switch's maximum gain provides a 9db peak at 6KHz. Or that the filter sweep tracks right through the sweet spot where that aperature/phase cancellation comb filter "hole" is. The goal is to recover the raw string information that disappears into the first few notches in the comb filter (and to boost those first few peaks that are -9db down from the fundamental), and to extend the instrument's electromechanical response up to where the strings themselves finally start to give up at 6KHz. Trying to push the filter by increasing the sweep range from 6KHz up to, say, 12KHz, would require a Q-switch with 21db of gain, followed by a six-pole low-pass filter, simply to push the amplified noise and RF back down by 36db or more. And the easiest way to create a six-pole filter is to use an "elliptical" filter, which happens to be exactly what the comb filter is, in the first place. Remmeber that the comb filter has peaks and valleys spaced all along the overtone chain from the fundamental signal. Put two of them in a circuit, and you'll get places where the peaks coincide. The technical term for that phenomenon is "oscillator." So, let's not go that way, and see what we can do to tame some of the peak-and-valley chaos that's already built into the mechanical comb filter. How about we simply squash is into oblivion? What do we lose? We lose the upper two octaves of a string that're already down -24db from the highest fundamental the bass will produce, and we lose any circuit noise generated in the pickups themselves or by the first preamp stages. We gain a measure of immunity from RF interference in the preamps, but more importantly, we gain that really neat 9db boost that exactly offsets the electromecanical filtering effect of the bass, AND, we get user-controllable support for the more significant nasties from the first few nodes of the electromecanical comb filter. So, we trade a hatfull of major headaches that occur above 6KHz for an instrument that gives you as close to a 100% accurate picture of what the string is actually doing as you're ever going to get with magnetic pickups. (For a look at the electromechanical comb filter in action, take a look at this really cool demonstration page by J. Donald Tillman. Also, take a run over to for a nice table of the Frequency of Musical Notes, from MichiganTech's Physics department.) Sorry to be so long-winded, but there's a huge amount of background to cover whenever you start trying to back-engineer Ron Wickersham. :-) nic | ||
| davehouck
Moderator Username: davehouck Post Number: 1954 Registered: 5-2002 |
Very nice Nic!! I enjoyed reading this! Tillman's applet is pretty neat too! | ||
| dnburgess
Senior Member Username: dnburgess Post Number: 422 Registered: 1-2003 |
Nic - great post - just the kind of thing to find a home in the forthcoming Alembic wiki - or should that be Alembiki. | ||
| alanbass1
Member Username: alanbass1 Post Number: 89 Registered: 4-2005 |
Should have heeded the warning, my head is spinning | ||
| jlpicard
Advanced Member Username: jlpicard Post Number: 211 Registered: 7-2002 |
Nic, Everyone should take the time to digest this info. After reading this post, the logic is inescapable as to why the filters are designed in this manner. I seriously doubt that there are many other manufacturers of basses out there that have given this much consideration to the design of their pickups and related electronics, etc. If there are, it is because once again, Alembic has pushed the envelope, and many manufacturers have jumped on the bandwagon over the years with one feature or another taking credit for themselves. | ||
| sfnic
Member Username: sfnic Post Number: 84 Registered: 3-2005 |
Sorry 'bout that, Alan. <g> Michael - In all fairness to (some) other manufacturers, there are quite a few people who have been researching the science of string vibration and nodal phase incident responses and so forth, for many years. But in a large way, you're absolutely right. Ron Wickersham learned and developed a lot of the underlying theory as part of his work in magnetics: remember that his pre-Alembic work at Ampex involved inventing, designing and debugging analog and video tape transport systems, and the multi-track recording heads and amplification systems used there. Aligning a 16-track head stack (especially when you're holding the first one ever built in your hands) takes a certain awareness of phase relationships and, especially relevant to our filter design example here, the effect of Cauer elliptical (comb) filtering on the audio spectrum. Before Ron's work at Ampex, _nobody_ had any idea of what effects such filtering might have on audio, or how any negative impacts might be overcome. Audio "printed" on mag tape suffers from many of the same problems that audio "printed" to ears of a listener suffer from, and many of the fixes are similar. Going from filtering the tape output to filtering an instrument's output isn't that far a leap, but ONLY if you've done both. In 1970, the number of people who had that experience were very, very few. Now, all that said, there was still a huge amount of research to be done in the various fields involved. It took Ron a tiny bit to get up to speed on the physics of string vibration and the properties of wood, but he had solid analogues in his magnetic and solid state electronics work, and he had the perfect research facility and colleagues available. But the contribution to the core theories made by people like Rick Turner, Frank Fuller, George Mundy, Jim Furman and many others cannot be overstated. The early definitions of filter breakpoints all came out of that original research, which was the first "lab" that ever considered both the electrical _and_ botanical _and_ mechanical issues in an inter-disciplined format. Every electric instrument designed up to that point had been simply tuned "by ear" to meet the designer's goal. Soon after, there were other people expanding on the research. Some passed through Alembic and many others were inspired by the possibilities. In many cases, individual breakthroughs came in specific areas of interest: Jim Furman expanded the original parametric filter into a complete product line (which in turn inspired Alembic's brilliantly integrated FX-1 preamp system). Jim's work spawned dozens of imitators, and even forced older, established players (Orban Parasound; Klarke Technik; White Instruments) to change direction. Bill Bartolini, Seymour Duncan and Larry DiMarzio all focused on making after-market and OEM pickups that would at least enlarge the range of options for players. Richard Schneider and Dr. Kasha did some outstanding work in desciphering the intracacies of string and plate vibration modalities. David Tarnowski (Analog/Digital Associates) combined Furman's filtering ideas with his innovative delta-modulation for inexpensively digitizing audio, and came up with the first viable digital delays, which were then expanded on by Lexicon and Roland and others. Luthiers like Ken Smith, Michael Tobias and others built on Alembic's early work and have defined pretty much the entire "tone library" we all use today in selecting recipies. Geoff Gould brought the first graphite neck concepts to Alembic, which opened the door for Ned Steinberger, Charlie Kamen and others to introduce composite materials into lutherie. (And we're only now really seeing the fruits of their original labor, in terms of graphite-reinforced necks, composite braces, hybrid laminated tops, etc.) And, to come full circle, a lot of the work with composites have allowed people like Rick Turner to completely challenge the classical notions of structural support within an instrument through the use of flying buttress bracing and lateral thrust members, which lets him expand on Frank Fuller's old work on plate vibrational nodes I mentioned above, to make some awesome-sounding acoustic instruments. There's been so much innovation in the past 35 years or so (not to mention the stuff done during the twenty or so years _before_ Alembic, by Leo, Christian, Orville, Seth and the other giants), that there's plenty of credit to go around. Would these things have been "invented" if Alembic hadn't been there to convince Jack and Phil and Dave that there might be a better sound lurking in those instruments? Probably. There were far too many people all thinking about the same things, right around that time or shortly thereafter. But there's no denying that there's a direct causal chain. Mike Doolin, for instance, makes some incredible acoustic guitars up in the northwest. But he'll be the first one to tell you he's built on Schneider and Kasha's work, and more importantly, that he's filtered _their_ research with what he's learned from Frank Fuller. Michael Tobias and Roger Sadowsky make great basses; but they didn't come into their own as a bass builders until they had hooked up with Alembic and the Alembic alumni at Stars Guitars. And any given month in Bass Player magazine will have a showcase builder who's designs or wood selections or electronic inspiration comes directly from the "Alembic school." Bill Bartolini would have been totally content building overwound humbuckers for Les Pauls, until he got his hands on an Alembic low-z setup. And EMG owes their entire existance to Bill's ability to make low-cost pickups and preamps that emulated Alembic's functionality, if not their consistancy or overwhelming quality (you have to cut some corners when you're trying to sell to the mass market). I've been exceptionally privileged to have worked with and for many of the above-mentioned people and companies. So I've actually ridden the "wave" of technological innovation that spread out from the old Brady St. digs and the Cotati farmhouse. That it's taken me 35 years to _catch up_ to what The Wizard and his team were doing way back then is a testament not so much to my own slowness in absorbing information, but rather in how freaking MUCH information was generated in those early years, and how much more has been generated since. It's an age of wonders, kids, and we're only in the infancy of What May Be. Who knows, maybe a 40th anniversary re-issue of Jack's #1, using Series III electronics? Or maybe jump directly to level 10 with a completely digital bass, along with its perfectly matched WiFi, DSP and amplification systems? We'll see... (Message edited by sf-nic on June 27, 2005) | ||
| sfnic
Member Username: sfnic Post Number: 86 Registered: 3-2005 |
Dave - Tillman's applet is awesome. See what happens when you keep enlarging the pickup aperature! | ||
| davehouck
Moderator Username: davehouck Post Number: 1957 Registered: 5-2002 |
Nic; when I "fret" the string, by moving the left end of the blue vibrating string, the yellow line that marks the note along the frequency scale moves as well, but the curve does not change. I must be missing something there. Otherwise, everything else seems to work and is quite interesting. Changing the aperature produces an unexpected result. It would appear that the narrower the aperature, the better the high end response. With two pickups, I find quite interesting how the relationship between the level controls changes the curve. | ||
| gare
Advanced Member Username: gare Post Number: 223 Registered: 11-2003 |
Nic Just wanted to say thanks for your wonderfully informative dissertations. I made a hard copy of the one above for future reference. You're a regular cornucopia of instrument information ! Keep em coming ! Gare | ||
| richbass939
Advanced Member Username: richbass939 Post Number: 313 Registered: 11-2004 |
Christopher, before we forget, welcome to the club. Your question started a great series of posts that are a good example of the wealth of knowledge that exists in this club. Personally, I like it when a young person is interested in Alembics. There are quite a few of us who were your age or older when Alembic started up and didn't have the chance to own one until much later. If you want, start a thread in the "Introductions" section and tell us about yourself and your musical interests. Rich | ||
| bob
Senior Member Username: bob Post Number: 466 Registered: 11-2002 |
Thanks for taking the time to give us such a detailed explanation, Nic. I'm on my third or fourth reading - of the first post with all the math. The more recent historical tour is also quite interesting, and may prompt some further research, but for now I'd like to comment on the earlier stuff. So what is the casual reader to take away from this? aside from perhaps a headache :-) My short summary would be this: Yes, technically speaking there is some energy in the strings above 6 kHz... BUT it is already ridiculously low in level simply due to the way strings vibrate, and even very low impedance pickups are going to be further rolling things off by that point, before we start thinking about further roll off by the filter. Using Nic's numbers, an overtone on an open G that is down by -45 dB around 6 kHz, just isn't worth thinking about. -45 dB is a LOT. While I believe that number is probably in the right ballpark, I might quibble or question a couple of things here. - Nic, you said "The pickup rolls off at 6db/octave from its resonant peak." Seems to me the usual value quoted here, for a pickup loaded with pots, cable, etc, is 12 dB/octave, as in a second order low pass filter. Was this just a typo, or can you clarify? - You also state that "The string rolls off at 6db/octave from the fundamental." I haven't seen it expressed in dB, but from my understanding of string behavior this seems low to me, meaning it should roll off faster and not necessarily with a linear slope. Now, we may not be thinking about the same thing here. Perhaps you are saying that if you play the note at the 12th fret, with the same plucking force or something, it will be down 6 dB from the open, and the 24th down 12? That seems unlikely, so I'm thinking we're talking about the relative strength of the partials of any particular note. If we put aside electronics for the moment and consider just the string, my understanding is that for a plucked string, the amplitude of the partials rolls off as 1/(n squared) where n is the partial, i.e. if you pluck a string such that it moves through a range of 1/4" at the 12th fret, then the 2nd partial will have an amplitude 1/4 of that, the 3rd will be 1/9, the 8th will be 1/64th, and the 30th would be 1/900th! On the other hand, for a struck string - as in a piano, and probably applicable to slapping a string against a bunch of frets - the amplitude decreases as just 1/n. Even so, by the time you get to the 30th partial of the 12th fret G (5.88 kHz), in theory it has an amplitude of only 1/30th of the fundamental. That's only the string, and I don't know how to express that decrease in dB. Also, if I understand correctly electric pickups tend to be somewhat more sensitive to frequency than amplitude, and may therefore recover more of the higher partials than would be "expressed" in an acoustic instrument. Anyway, I don't mean to argue, just curious about this stuff. In regard to one of the questions here about whether it matters, I was reminded of a couple of earlier discussions on the subject. In a moment of indiscretion, I went so far as to suggest that for bass purposes only, buying a cabinet that is rated only up to 6 kHz was a perfectly reasonable thing to do (and have done so, with no regrets). Somewhere a bit down in this discussion Dave is quite certain that stuff as high as 12 kHz is an important aspect of his tone, while in contrast Thomas (poor_nigel) talks about an experiment in building his own cabinets, that resulted in removing the horns he had already purchased because he found nothing useful coming out of them. -------- Moving right along...:-) Tillman's demo applet is indeed quite interesting. I downloaded the code and made some small enhancements for my own purposes a couple years back, and learned some interesting stuff. So I'd like to emphasize a couple of points to help prevent misinterpretation of the graphs. First of all, the chart does *not* show you the response that you are actually getting from the pickup(s). If you don't think about that, and just look at it, you might find yourself saying, Wow, look at all that stuff going on way up at 10 kHz! If you doubt this, try "playing" different notes on the fingerboard at the top, without changing anything else, and you'll see that the plot doesn't change in the slightest. Also note his disclaimer, that it "does not show the effects of the pickup's electrical parameters (inductance, capacitance, loading, etc.)", so it does not reflect the fact that above pickup resonsance - say in the range of 3-6k - the pickup will be rolling off the response quite a bit more. If you're interested, we can look at a few examples. Aside from general curiosity, I spent some time with this program trying to help me figure out whether I might prefer FatBoys to MXYs, or whether I might prefer a different location for the neck pickup. For starters, here's a way to get a more visual or intuitive grasp of this comb filtering business (I haven't needed a comb in so many decades that this is a difficult concept for me...). Here's the plot you get for my bass with a FatBoy in the neck position only (not using the bridge). The numbers are a bit approximate, but my pickups are in the standard position Alembic uses for a 35" scale Rogue; I used a width or aperture of 1.5" for a FatBoy (or Series) and .75" for an AXY/MXY: 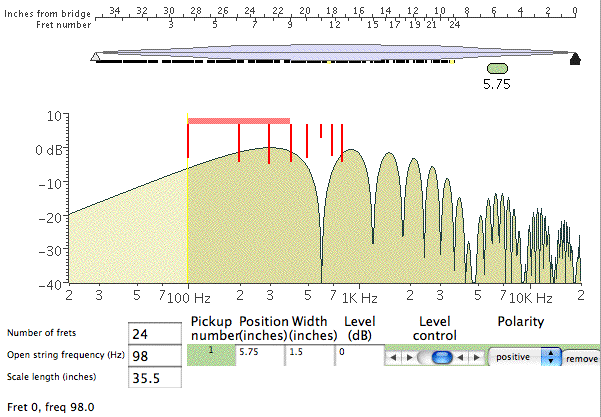 and here's an easy way to see where the notch around 600 Hz comes from: 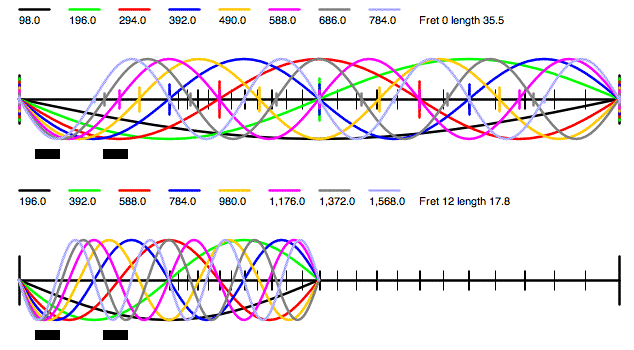 The plot on the top shows the first eight partials of the open G string. Note how the 6th (pink) at 588 Hz has a node or null point nearly centered over the neck pickup. That means the pickup can't really "see" this frequency, hence the first notch around 600 Hz. The bottom plot, fretted at the 12th, shows the same first notch (now red), and a second one (pink) around 1200 Hz, also visible in Tillman's graph. By the way, this is essentially just what the program does. It loops through the range of frequencies, figures out what the shape of the wave is above the pickup, and sums the amplitude at each point over the pickup. So if the wave is either fully above or below the axis then you get a large value, while if it crosses the axis within the pickup width you get some cancellation, equating to zero if the crossing point is dead center. Though I may have missed it (don't think so), he makes no attempt to adjust for decreasing amplitude in higher partials, partly because he isn't working with partials per se, but also based on his statement in a referenced article that magnetic coils are more responsive to higher frequencies than larger amplitudes, "so it all evens out" (not a direct quote, but close). While I think that might be fine as a first approximation, my guess is that it significantly overstates the response above around 1-2 kHz. What I believe you see in these charts assumes that even up at 10 or 20 kHz, the string is vibrating in a way that *could* produce as much output from the pickup as the open fundamental. Though it's useful to look at it this way within the range of notes you can actually play, it becomes unrealistic at the higher frequencies. Back to the charts with all the sine waves, note how much less confused things are down at the bridge pickup, which is evident in the Tillman plot for just a bridge FatBoy - the first notch is all the way up around 2 kHz, because that's the frequency at which you first get a null/node over the bridge pickup: 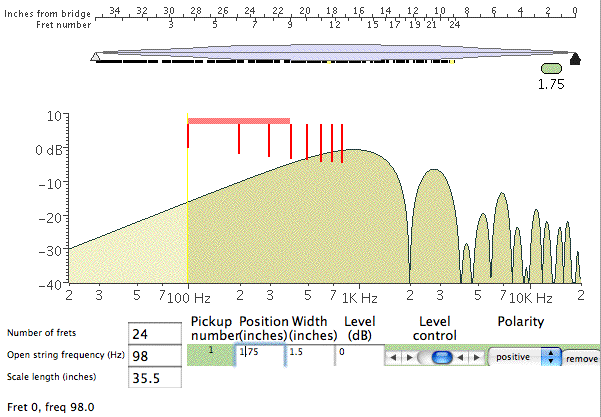 In case you're wondering about those vertical red lines, I added them to show the frequencies of the first eight partials for the selected note. The original horizontal red bar shows the two octave range available for the string (24 frets), while the new vertical bars help to visualize how the early partials of any particular note line up with the response curve. If you were actually looking at a plot of the response for a a particular note, the chart would be mostly empty with sharp peaks where each of these red vertical bars appear, plus more to the right for the higher partials. Disregard the exact height of these lines - I wasn't interested enough to figure out the math, so they all start as a constant height and just get scaled by the response. But you can see in the first plot that the 6th partial is greatly reduced by the bridge notch, perhaps more than appears here, and of course all of them would be decreasing drastically even before considering the pickup response. One last Tillman plot, that was helpful to me. This one uses both pickups. The regular plot (tan-ish area) assumes wide aperture (FatBoys or Series) in both the neck and bridge positions, while the blue outline show the response after replacing the neck FatBoy with a narrow aperture (MXY) centered in the same spot: 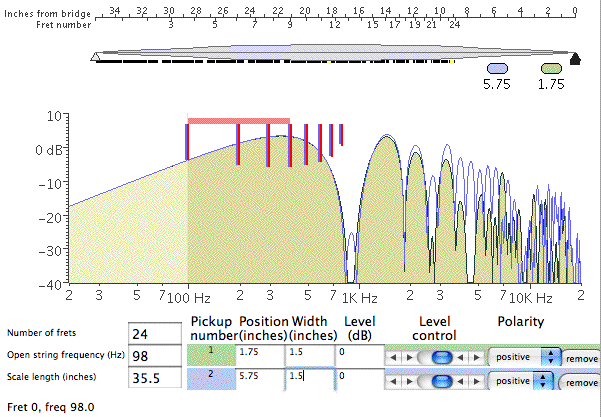 Notice how the narrow aperture at the neck helps a lot to fill in the gaps, and is consistent with my preference for this combination. If I ever built another custom, I would probably move the neck pickup closer to the bridge to further even out the response (you can always add more bass with a SuperFilter). ----------- Finally, one more question/comment for Nic. In regard to the 9 dB Q switch gain, you state that "The goal is to recover the raw string information that disappears into the first few notches in the comb filter". Well, maybe, but I'm quite skeptical about both the implied motivation on Ron's part, as well as the effectiveness. The main problem I have with this theory is that the notches are significantly different for each of the pickups, and furthermore for each of the strings (on each pickup). Here are the approximate positions of the first notch, for strings EADG, separately for each pickup, and combined with both pickups (both assumed to be wide aperture in standard positions): neck: 250, 330, 450, 590 bridge: 830, 1100, 1470, 2000 both: 370, 500, 650, 850 With two pickups, even the 8th partial doesn't get up to the second notch until you're playing above the 13th fret or so. For just the bridge pickup, the 8th partial won't fall into a notch for any note you can play, although for neck only the 8th falls into a hole when you play at the 7th fret, and you find the 3rd notch if playing the 14th fret. So where am I going with this? - Let's assume for the moment that the tone you actually end up hearing, is shaped almost entirely by the first 8 or fewer partials. I think this is actually somewhat generous, though no doubt some will disagree, and I'm interested in "hearing" any serious counterpoint. - If that's a valid assumption, then if you are using an even balance of both pickups, the second notch doesn't affect you until you are playing above the 12th fret. - The notch you have to contend with ranges from around 370 to 850 Hz, depending on which of the four strings you happen to be playing. Now, you might *conceivably* try to use Q to fill in such a notch, but would encounter at least the following problems: - you could only do so for a single string - you would have a very difficult time dialing it in that precisely - setting the filter frequency low enough to cover any one of these four points would have already grossly colored your sound, not helped to even it out. Look, I'm not trying to be difficult or obnoxious, but we are talking about physics and lots of numbers here, and I think it's important to review carefully. While the magic of the 9 dB number seems to work out conveniently with some of the math, I don't buy the suggestion that it is there to deal with the notches in the response curves, or more generally to help even out the pickup response - which would imply you should leave it on all the time, at some particular frequency, to get the most even response, except that it won't do so as noted above. My personal guess is that the value was chosen largely because it provides for an interesting variety of *uneven* responses, depending on where the frequency is set. It makes for an interesting tone shaping device, not a solution for the uneven response due to comb filtering. But hey, I've been wrong before, so please feel free to straighten me out. -Bob | ||
| byoung
Member Username: byoung Post Number: 99 Registered: 12-2004 |
I'm thinking a duel might be the best solution: How about slide rules at 10 paces? I'll second. Brad | ||
| jlpicard
Advanced Member Username: jlpicard Post Number: 215 Registered: 7-2002 |
Definitely a "Clash of the Audio Titans". And Dave, absolutely one for the "Faq and Must Reads" section! Mike | ||
| davehouck
Moderator Username: davehouck Post Number: 1964 Registered: 5-2002 |
Mike; done. | ||
| bob
Senior Member Username: bob Post Number: 467 Registered: 11-2002 |
You know, I'm pretty sure I still have a slide rule here - somewhere, in a box out in the garage, would take me hours to find... It was handed down, perhaps lovingly, by my father - about 14 inches, very fine quality (probably German), and came with a fine leather holster that you could actually mount on your belt. I swear I never did so, but I'm old enough to have been actively using it throughout high school, only switching to a calculator during my first year of college, when there was still some dispute about whether they were legal for use during exams. Based on the demographics of the club, this will probably be vaguely familiar to many of you :-) So what do we do now, at 10 paces? Set them on stun and hurl them at each other? (and Brad, are you any good with these things?) Just a gentle reminder, folks - it's not about Who is right, but What is right. Some of this stuff is really complicated, can be looked at from extremely diverse and sometimes conflicting angles (electronics vs. acoustics, for instance), and much of it is still not well understood, even here in the glorious 21st century. Nic has brought a very welcome scientific/experimental perspective to a number of discussions here, but he's still subject to peer review - and I expect he wouldn't want it any other way. We all have lots to learn, and it's a fascinating area. I look forward to further discussion. PS: I should also formally thank Mr. Tillman for publicizing the source code for his program, because it was much more useful to me after a few simple modifications, and I borrowed some of it, for the math behind the colorful sine waves based on fret position. Thanks. | ||
| keith_h
Intermediate Member Username: keith_h Post Number: 109 Registered: 2-2005 |
Bob, Yes the great calculator controversy. Went through it in high school. We were encouraged to learn to use them in class but could not use them for tests. However we were allowed to use slide rules on tests (circular or linear). Then I brought my National Semiconductor 100 step programmable to class one day and was told I couldn't use it at all. Didn't matter I had to know the formulas to program it they said it was cheating. The description of your slide rule sounds identical to mine including it being an inheritence from my father. Keith | ||
| fmm
Member Username: fmm Post Number: 90 Registered: 6-2002 |
I've got my Post Versalog 1460 right on my desk. It scares the hell out of my boss when I use it. I've got several others in my desk drawer. Combine that with my HP 41CX calculator (no = key) and my touchpad (no mouse); my boss hates coming to my desk. She can't make anything work. I also have a 7 foot teaching sliderule in my basement. | ||
| gare
Advanced Member Username: gare Post Number: 224 Registered: 11-2003 |
Can a slide rule penetrate one of those new kevlar vests? And that 7 footer should be banned from the games..someone could get hurt if you drop it ! This is a great thread ! I know I have a ton to learn on this subject..like Bob just said it's not who but what is correct. Another related topic that's always interested me was what can human hearing actually hear or perceive ? Who can actually hear 20hz to 20k hz ? Ok..that's another thread. Back to the duel ! | ||
| richbass939
Advanced Member Username: richbass939 Post Number: 314 Registered: 11-2004 |
I don't know what my hearing range is but my wife is convinced there is a dead spot somewhere in the middle. Does anyone know the frequency range of the voice of the average human female, any devices that might enhance my perception in that range, and where I might buy one? Rich P.S. Fantastic thread, BTW. | ||
| sfnic
Member Username: sfnic Post Number: 90 Registered: 3-2005 |
Dave - The applet display seems to work off the open string frequency, regardless of the fret position selected. It may be browser-dependant; I've only tried it with MSIE. For Bob, some clarifications: yes, the classic pickup-to-amp-via-cable model says 12db/octave. That's because you're considering both the capacitive and inductive reactances of the system. Two reactors, two "poles." I had started my post from the perspective of ignoring the interior loading of the instrument's controls and the cable and the amp's impedence, and forgot to add those losses back in. The reason I didn't consider them initially is because the Alembic filter's output driver is intended to minimize cable effects. Driving the cable via an opamp output makes the source impedence very low, so the RC and RI reactance poles there are well out of the instrument's passband. Since I was playing with the instrument's mechanical performance, I kinda forgot about the downstream factors. <g> (I also basically ignored the pickup's own C/I poles, figuring that Tillson had included them generically in the applet to generate his response curves, and so adding them again might be redundant.) Overall, I'll stand by the 6db/octave initial slope _from the pickup_ because I'm only really looking at the R impedence pole, and because in the Alembic filter, the pickup loading isn't from the pots, it's from the FET buffer amp. Yeah, there's 6-8" of shielded cable from the pup to the FET, and there's definitely a measureable effect on the pup's response. But it's been designed to be as minimal as possible, so for the sake of looking at the following filter, I threw it out altogether. My statement about the string is based on simple free-space wave decay, absent any other environmental factor. That's equivalent to a single-pole filter because inertia is the only reactive component. A string deflection at the fundamental equals 1. The 1st node harmonic's (one octave above fundamental) maximum deflection is .5, or -6db. Looking again at Bob's note: 1/(n squared) for a plucked string. Hmmm. Inverse-square law, based on pre-loading the string with a lateral deflection of 1 Zero energy from the initial displacement; 100% energy applied in restoring the string to a rest state. You may well be right. I was working from a simpler 1/n for the struck string (initial lateral deflection of zero; 50% of the energy consumed in placing the string into motion, the balance expended returning to rest), as there's only one pole involved. I'd need to go back and check. I'd assumed 1/n, as that sums out to a .707 max deflection at the string's midpoint, when you run the sum-and-differences all the way out. But 1/(n squared) may indeed be correct, as it deals with ultimately with amplitude of deflection, as opposed to energy expended. <musing> And, of course, that calculation chain refers to the free-space characteristics of a vibrating member supported by two fixed endpoints and affected by no other environmental factors. And, equally of course, real-world string vibration is a bit different. On a bass, the string isn't vibrating in free space and the endpoints aren't fixed. Each endpoint is capable of providing secondary impulse drives to the string-in-motion. What those secondary drives are and how they're applied to the string are major components of the overall tone we hear, as they drive frequency-and-phase-related energy back into the string. In general, however, that re-applied energy is less than the original impulse. So the string vibration does, in fact, decay. Should the re-applied energy exceed the string's own vibrational inertia, however, it can force a sustained vibration with deflections potentially greater than 1, up to the modulos of elasticity limitations of the vibrating structure. At that point, there's either equilibrium (a sustaining oscillator) or traumatic deformation (the Tacoma Verazano-Narrows Bridge, for instance). So, to keep things simple and to isolate the instrument's body effects from the raw string, based on 1/n I took 6db/octave for the string's raw harmonic curve. The curve won't be steeper than that, free space, and the idea was to see how the primary drivers of pickup position and aperature affected the baseline. Adding in re-applied energy at the bridge/sustain block and nut/peghead/neck deflection endpoints simply add in additional elliptical filtering. I suppose that, assuming only two supplemental drivers acting in-phase at any given frequency within the string's harmonic structure, you could see vibrational transients of up to 4 x .707, or 2.828 times greater than the initiating deflection, or about 9db "hotter" than the fundamental. But that's only if the endpoint drivers are each _capable_ of driving the string with the 4x the energy of the initial deflection. I'd assume that, because the source of the re-applied energy is the string itself, even 100% efficiency in reflection would merely keep the string at a 1:1 equilibrium, at best. And that, only at the fundamental. The overtones would still decay at an average rate of 6db/octave. Now, add in a third energy re-application source (vibrating air from a loudspeaker, for instance), and things can get a bit out of hand... </musing> Now, in the speaker selection discussion, while I can see both sides, I personally do find that there's useful energy from a bass guitar above 6KHz. Purely in the pick or finger attack, if nowhere else in the string mechanics. The attack impulse takes place perpendicularly to the string axis, and has the effect of both striking and plucking the string. This is more pronounced on a bass than on a guitar, as it's dependent on the duration of contact with the string from the initial impact to the final release. IIRC, that duration falls somewhere between 1 and .1 millesecond (1 KHz to 10 KHz). There are also abrasion effects as the finger or pick crosses windings. Again, IIRC, these "mini-strikes" take place in the range of beween .2 and .02 ms, or 5KHz to 50KHz. Which is a long-winded way of saying that there's a "click" on the attack that occures somewhere generally above 5KHz. More so with picks than with fingers; even more so with round-wounds than with flats. I like to get that click out there; hence my preference for JBL 5s and EV T350s. :-) That said, I often discovered that the mid-range 12s in my rig were essentially MIA (when playing bass through them). There was _some_ info in there, but I could drop them out and run 15s and 5s with virtually zero change in bass tone. (But then, I EQ most of my bass' midrange away completely. There's basically a dead zone from maybe 800Hz up to about 4KHz. But I _like_ it that way, for some ungodly reason. On to Ron's motivation for the 9db Q-switch: I haven't a clue. It may well have been a case of asking "how much gain do we want?" and then tweaking it until it sounded right. That would have been the ultimate criteria, in any case; my reverse-engineering exercise was intended merely to see what there was above 6KHz. What I found was a notch that happens to generally coincide with the filter's response. Now, the early filter work, using Ron's initial filters on Dave and Jack's instruments and the giant spaghetti pile Gumby stuffed into Phil's bass, created a set of test beds. Figuring out what worked best was partially a trial-and-error effort, but it definitely had a starting place grounded in the application of string mechanics. It's a key reason Jack's bass had variable aperature pups that could be moved. The designers had a pretty good idea of the range of parameters they wanted to cover, and Jack was a willing guinea pig in determining what sounded good. Once he nailed it down the settings, Ron measured them, plotted them against what he already had on the mechanical response of the bass, and basically said, "this is what's useful; we'll build it like this." And then went off and designed the "production" Series filters. Now, my own feeling about the "6KHz notch" is that if you're looking for the highest useful sound the instrument will make, you start with the highest fundamental the instrument will produce. That's a 392Hz "G" note, 24th fter, G-string. Even a simple 1/(n squared) analysis of that note shows the G at 6271 Hz is only 1/16 the amplitude (-18db) of the fundamental, without even looking at the comb filter. Add in a "spit into the wind" estimate that pickups are rolling off somewhere around there, and take a look at electro-thermal noise generators, and 6KHz starts to look real good for a filter top-end. Add in a gyrator-sourced resonant peak at the top end, just before you kick the response off the cliff, and you get the pick/finger attack back. Listen to Jack's solo in Feel So Good off of 30 Seconds Over Winterland, and imagine that tone without a Q-switch boost, or with the filters rolled back. (Jack was playing flat out on that solo; the bass was giving everything it had, frequency response and output power-wise). I bring that up not to throw it in anyone's faces, but as a sonic example most everybody here will be familiar with. That specific tone, albeit preferrably not quite so amp-overdriven, is the one of the key tones used as models for the production Alembics. Now, all that said, I _think_ I just agreed with Bob's ultimate point about the Q-switch and the "6KHz notch." If that's not clear (and it probably isn't <g>), let me restate: I happened to find a convenient correlation between ONE ASPECT of the complex electro-mechanical model that is an Alembic bass, and ONE ASPECT of the overall filter design applied to that electro-mechanical model. The ONLY justification I have for assuming any _direct_ correlation is that I used one endpoint datum as definer of the extreme limit condition, and noticed that the filter's designed conveniently covered that endpoint case. That assumption of correlation carries absolutely zero water when considering non-endpoint cases of the e-m model, as Bob is exactly right in pointing out. Bob suggestion that "the value was chosen largely because it provides for an interesting variety of *uneven* responses, depending on where the frequency is set. It makes for an interesting tone shaping device, not a solution for the uneven response due to comb filtering" is absolutely correct, when evaluated in light of the actual design process. (And he's also dead-on about peer review!) :-) nic | ||
| sfnic
Member Username: sfnic Post Number: 91 Registered: 3-2005 |
(And somewhere in his upstairs office, Ron is undoubtedly laughing his ass off at all this noise over what was essentially a techno-artistic design decision that probably took all of 30 seconds to make...) | ||
| davehouck
Moderator Username: davehouck Post Number: 1968 Registered: 5-2002 |
Nic; I believe that would be the Tacoma Narrows Bridge (the Verrazano-Narrows Bridge being in New York), and I definitely don't want my bass doing what it did! And, I don't have a copy of Feel So Good and no longer remember what it sounds like. So if anyone might have a good MP3 I could borrow for a few minutes <g>. | ||
| dadabass2001
Advanced Member Username: dadabass2001 Post Number: 399 Registered: 6-2002 |
Man....! Now I gotta go out tomorrow to Best Buy or Tower to search for "30 Seconds over Winterland". I had the LP in the dark ages, but it left with the wooly mamoth and I don't remember the solo either. Was that sans Spencer? I had true sonic joy in the Spencer years. Sorry for the OT moment. I'm still with you, although my eyes are glazing over. That might just be post-rehearsal decompression.  Mike | ||
| bigredbass
Senior Member Username: bigredbass Post Number: 429 Registered: 9-2002 |
I've always felt that horns in bass cabinets were just not necessary. This business is certainly 'me too' driven, and after the inital wave of Trace/Elliot and SWR success, it was no surprise to me that every bass amp/cabinet manufacturer just HAD to jump in, and often in many cases I'm sure just slapping a horn in the cabinet in the left over space on the baffle board with not much more than the cheapest Zalytron/Radio Shack crossover that the bean counters would allow after the NAMM hangovers wore off. For several years I worked for a small touring sound company, running your basic three-way tri-amp PA for 5 to 10,000 seaters. I NEVER heard much bass in the middle pass or the horns, and never saw it in the RTA shots during the shows. We had old school w-bin 18's for subs in those days rolled over at 250hz, and of course the rest of the bass was in the low end of the mid bins, but not the meat, not the bottom that anchored the band and locked with the kick. When I first moved to Nashville in 1990, I saw this scene repeated over and over: The bassist had a Modulus or a Pedulla w/Barts or a Tobias, etc. running through a Hartke or Trace or SWR stack. And they all sounded just like this: LOTS of mids with NO bottom to anchor the band. How do you dance or even tap your foot to that crap? That sort of tone might work for Entwistle, but look at the 'rest of the story' at a Who show: World class PA and FOH engineers, and rabid fans. It just DOESN'T work at the juke joint out on Highway 61. I often think this ball-less bass is why you see so many Jazz Bass/SVT rigs these days, people subconsciously realized that you need concrete to stand on, not rice paper. This is why f2b's, SVTs, Bass 400's, Demeters, will always be steady sellers: There's always a group of people who just wore themselves out with PAs for bass rigs, plug into a f2b/Crown/15 cab and say 'why have I been killing myself? This is IT.' I've always wanted a sophisticated version of Jamerson's PBass/FlipTop sound: Not quite so lumpy, enough articulation to be clean, but without enough top end to grate on your nerves. And going up to 5 or 6k is plenty to do just that to these ears. J o e y | ||
| byoung
Member Username: byoung Post Number: 100 Registered: 12-2004 |
Joey, I'm with you on the horn tweeters. I haven't heard a horn tweeter that I like. They all seem to make everything sound like it's being played through a cymbal. My thinking is that if you're into all that high-frequency stuff (at the expense of a fat bottom), maybe you should be thinking about getting one of those custom light-gauge, 25.5 inch scale 6-string basses. Now for another question: what is the cutoff frequency on a series guitar? Brad | ||
| bob
Senior Member Username: bob Post Number: 469 Registered: 11-2002 |
Rich - I expect you were just joking, and I'd prefer not to speculate on the nature of devices you might buy that would cause you to be more responsive to verbal requests from your wife (ouch). But if you have some serious questions about various forms of hearing loss/impairment, you should start another thread. There was some good stuff here recently on tinnitus, which is a fairly specific problem; males generally suffer from reduced high frequency perception with age, while the classic "too much exposure to loud stuff" problem tends to result in a scoop in the low thousands region. Joey - obviously, I'm with you. If you want to sound like a bass, be it an upright or maybe classic Motown with a bit more articulation, you don't need horns or tweeters. At the same time, if your style demands that you hear the sounds of calloused fingers scraping across thin gauge, round wound, stainless strings, or strings bouncing off frets, then go for it :-) I don't mean to sound cynical or sarcastic, slap and maybe some picking techniques that emphasize the attack *mechanism* (not to say the more general attack envelope of the tone) are valid reasons for wanting some higher frequency output. Just not mine. Dave - I don't have a copy of the referenced Feel So Good either, and it's not quite enough for me to open an iTunes account just to get one song (if they have it) that I might listen to twice, at most. Though I am adamantly opposed to piracy and will not copy stuff for friends, something like a 30 second excerpt strictly for educational/reference purposes falls within my understanding of the definition of fair use, and would not concern the labels. So if you happen upon a good quality excerpt, I'd also be interested. Dave again (and Nic) - the "yellow line" problem, of the applet not being sensitive to the selected fret position, is neither a bug, nor a deficiency, nor a browser issue. I said something about this in my post, though indirectly and it was written before Dave asked the question: - The program just shows the theoretical response of pickups at certain positions, ignoring electronics and tons of other details. It just figures out how waves pass over a given position (the pickup), and I still think it assumes they all have the same amplitude. - For a string tuned to any given pitch, the wavelengths of all frequencies you can produce on that string, regardless of where you play and including all partials, are fixed. - Since the bridge is in a fixed position, and determines one end of the waves, the only thing that matters then is how far the pickup is from the bridge, and how wide it is. This was not intuitive to me either, and one of the first things I started to do after downloading the code was to figure out how it could be "fixed" to reflect what happened as I played different notes. Well, I got to the right place in the code, and (though I can't be absolutely certain) it looked like Tillman had started to write something there, quickly realized it didn't matter, and commented it out. This in turn prompted me to look at the frequencies and wavelengths, for partials of various notes. It's an interesting result, and a good reminder that while the wavelength of a low B in room temperature air is on the order of 36 feet, it can be more like 36 inches or less in a heavy metal string (not a reference to musical preference). Nic - thanks for the clarifications, further insights, and yet more historical footnotes. Let me be the first to admit that some of this is over my head, and it's also probably more than most of us need to know - but interesting, and thankfully I seem to keep learning stuff. I don't consider myself to be your peer in either the electronics or more general mechanical physics realms, but sometimes I can spot what appears to be a logical or practical flaw in reasoning, and hopefully ask a good question. My main point was just as you said: while Ron has done some truly brilliant work, and I will personally be forever indebted for what he did on my bass, I think he'd get a pretty good laugh at the suggestion that he should file a patent for solving the comb filtering problem with a 9 dB Q switch. Now, I'd really like to hear Jack's solo (just for reference of course). Wait, one last thing for tonight... Going back to the key practical question: how many classic guitar amps (which certainly need a higher range than for bass) can you think of that had nothing smaller than 10" drivers? Yes, nowadays you can get around 6 kHz out of these, but still not a lot more. I'm too tired to research the question, but if we take a relevant example like the Wall Of Sound - what was the high end response of the portion used for guitars? -Bob | ||
| dnburgess
Senior Member Username: dnburgess Post Number: 426 Registered: 1-2003 |
Nic - glad you mentioned the percussive noises that come from a bass - especially with slappin' and poppin'. Subjectively, these noises seem to be in about the same frequency range as hi-hats - say 12kHz to 18kHz. That alone seems like good enough reason to have a rig capable of reproducing information above 6kHz. David B. | ||
| goatfoot
Member Username: goatfoot Post Number: 71 Registered: 12-2003 |
You can listen to a 30 second snippet of Feel So Good at the Allmusic site. Here. It's not Jack's solo, unfortunately, but you can hear how his bass sounded. This is a great thread! I don't understand half of it, but it's great. Kevin | ||
| bracheen
Senior Member Username: bracheen Post Number: 756 Registered: 11-2003 |
Here's a 47 second file of Jack soloing. http://www.hottuna.com/archive.htm | ||
| davehouck
Moderator Username: davehouck Post Number: 1972 Registered: 5-2002 |
Based on some of the above comments, I'm guessing that several of our group would not like to hear me play my bass <g>! But that's entirely reasonable; there is a lot of music that I don't care to listen to either. Bob; just for reference of course! Bob; on the "yellow line" issue, I tested your statement. I entered 34" scale and 55Hz, open A string, and printed the graph. Then I entered 25.5" scale and 73.42Hz, D at the fifth fret on the A string, and printed that graph. The curves are very close to being identical. | ||
| bob
Senior Member Username: bob Post Number: 471 Registered: 11-2002 |
(Disregard this post, I don't know what I was thinking, but it was wrong. Just changing freq and scale length as Dave did appears to give identical plots until you get over about 5 kHz and start seeing some small differences.) To get the curves truly identical (within pixel math resolution), you would also need to scale the position and width of the pickup(s) by 25.5/34, in other words shrink everything identically. (Message edited by bob on June 30, 2005) | ||
| alanbass1
Member Username: alanbass1 Post Number: 90 Registered: 4-2005 |
Nope, my head has totally gone now | ||
| bracheen
Senior Member Username: bracheen Post Number: 758 Registered: 11-2003 |
At least you hung in Alan. I think Christopher bailed after his third post. | ||
| sfnic
Member Username: sfnic Post Number: 93 Registered: 3-2005 |
:-) |